User-Defined Molar Volume Database
The molar volume (Vm) is one of the pre-defined properties in Pandat™. The molar volume of a pure component is described as a function of temperature and pressure, and the excess molar volume of a phase is usually described in the format similar to that used to describe the excess Gibbs energy of the phase. Note that, if a phase is described by a compound-energy-formalism (CEF) with multi-sublattices, the molar volume is automatically described as a function of T, P, and site fraction (y) following the format of the Gibbs energy. This will introduce many end members in the molar volume and may lead to incontinuity in the calculated molar volume. In reality, molar volume should be a function of mole fraction (x) instead of site fraction (y), it is thus recommended to define the molar volume of a phase separately from its Gibbs energy if the phase is described by the CEF model. This can be realized through the user-defined molar volume property.
In brief, the molar volume of element i with crystal structure f can be expressed as:
|
|
(1) |
where V0 is the molar volume under atmospheric pressure at the reference temperature T0. And a is the coefficient of linear thermal expansion (CLE). The volume of a phase with crystal structure f can then be obtained via the Redlich-Kister polynomial:
|
|
(2) |
where xi is the mole fraction of element i and is the excess molar volume. Using ternary system as an example, the
can be expressed by:
|
|
(3) |
The terms and
are the interaction parameters from the constituent binary and the ternary systems, respectively. The standard unit of molar volume is m3/mol-atom.
The molar volume database also enables us to calculate the density based on the relationship of (r is the mass density, M is the molar mass, and Vm is the molar volume).
Here we use the Al-Ni binary system as an example to demonstrate the calculation of molar volume through User-Defined Property. Please refer to the AlNi_Vm.tdb for details. In the beginning of the database file, a Type_Definition is given as below:
Type_Definition v GES AMEND_PHASE_DESCRIPTION * VARIABLE_X Vm !
In this definition, “v” is the identifier, “*” means any phase, and VARIABLE_X is the key word indicating X as the variable. The meaning of this definition is that any phase with the identifier “v” will use mole fractions (x) as the variables for Vm. Here are examples to define the molar volume parameters for the Fcc and L12_FCC phases in the Al-Ni system:
Phase Fcc %(v 1 1 !
Constituent Fcc: Al,Ni:!
Parameter Vm(Fcc,Al;0) 298.15 +V_Al_fcc; 3000 N !
Parameter Vm(Fcc,Ni;0) 298.15 +V_Ni_fcc; 3000 N !
Parameter Vm(Fcc,Al,Ni;0) 298.15 -2.85e-6; 3000 N !
Phase L12_FCC %v 2 0.75 0.25 !
Constituent L12_FCC: Al,Ni:Al,Ni:!
Parameter Vm(L12_FCC,Al;0) 298.15 +V_Al_fcc; 3000 N !
Parameter Vm(L12_FCC,Ni;0) 298.15 +V_Ni_fcc; 3000 N !
Parameter Vm(L12_FCC,Al,Ni;0) 298.15 -3.2e-6; 3000 N !
Even though the L12_FCC phase is modeled by CEF model with two sublattices, four end members, and 13 interaction parameters, its molar volume property can be described as a function of xi like a solution phase through User-Defined Property. In other words, the molar volume of L12_Fcc is:
|
|
(4) |
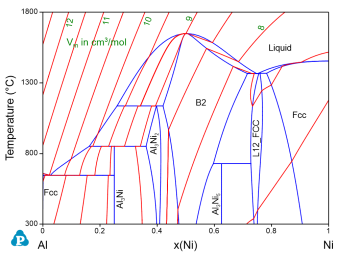
Figure 1 shows the calculated Al-Ni binary phase diagram with molar volume contour lines. Please refer to AlNi_Vm.pbfx and Section Contour Diagram for details on the calculation of contour diagrams.
The lattice constant, or lattice parameter, refers to the physical dimension of unit cells in a crystal lattice. For FCC crystal structure, the lattice constant can be calculated by:
|
|
(5) |
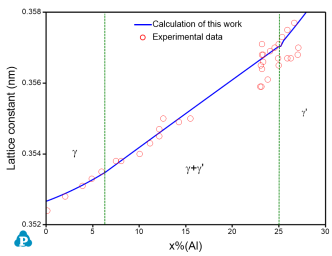
An example is given for the calculation of lattice constant in Ni-Al binary at Ni-rich corner. The calculated lattice constant agrees with the experimental data well as shown in Figure 2. Please refer to AlNi_lattice.pbfx for details. It should point out that the unit of Vm in the above equation is cm3/mol.