吉布斯自由能的Hessian矩阵
Pandat™ 可以计算一个相的吉布斯能量的Hessian矩阵的行列式以及Hessian矩阵的特征值和特征向量。
对于组元的摩尔分数变量 (x1,x2,⋯,xn) 而言,有一个组元的摩尔分数是因变量。当某一个组元的摩尔分数为因变量时,它是由其它组元的摩尔分数共同决定。在不失一般性的情况下,选择 xn 作为因变量,即将最后一种组分考虑为溶剂。然后,一个相的吉布斯自由能的二阶导数形成一个Hessian矩阵,它是一个 (n-1)×(n-1) 对称矩阵。
其行列式为
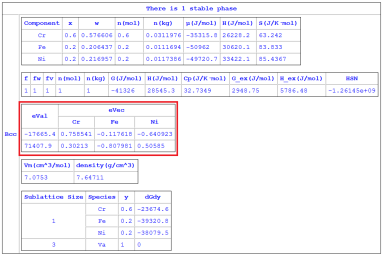
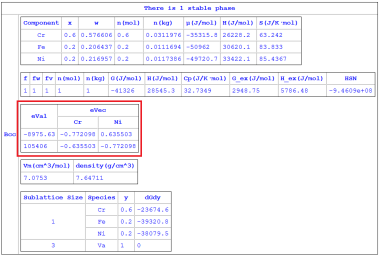
f相的Hessian矩阵的行列式可从“HSN(@f)”获得。“HSN(@f)”的值与溶剂组元的选择无关[2021Mor, 2022Che]。
Hessian矩阵具有真实的特征向量,每个特征值都有一个对应的特征向量。特征值及其特征向量可从“eVal(#*@f)”和“eVec(*#*@f)”获得。前面的Hessian矩阵具有“eVal(#1@f)”, “eVal(#2@f)”, … ,“eVal(#n-1@f)”的特征值。每个特征值都有一个特征向量。例如,eVal(#1@f)的特征向量为(eVec(C1#1@f), eVec(C2#1@f), … , eVec(Cn-1#1@f)),其中Ck为第k个组元的名称。关键词HSN, eVal 和 eVec的含义详见 Pandat™表格中的语法格式 中的表 1。
“溶剂”组分可以在使用菜单栏中“Property → Thermodynamic Property” 弹出的条件设置界面中定义,也可以在批处理文件(.pbfx)中定义。例如,可以在批处理文件中添加“<solvent name="Fe" />”,以选择 “Fe” 作为溶剂元素。如果未定义“溶剂”组分,则会使用一种特殊处理方法(称为正交化[2022Kon]), 以确保特征值和特征向量与溶剂组分无关。这种特殊处理方法在分析高熵合金中的调幅分解非常有帮助。请注意,为了提高计算效率,在常规的热力学计算中不会计算特征值。用户可以通过在批处理文件中添加命令“<Hessian value="true" />”来计算特征值。在示例文件夹(\Pandat 2024 Examples\PanPhaseDiagram\Eigenvalues)中可以找到通过选择溶剂( Eigenvalues_solvent_Fe.pbfx)或不选择溶剂元素(Eigenvalues_nosolvent.pbfx)计算特征值/特征向量的批处理文件例子。
利用Hessian矩阵特征值计算调幅分解线
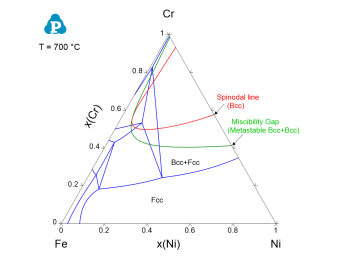
Gibbs自由能的Hessian矩阵特征值的重要应用之一是计算调幅分解线。可以将eVal(@*)作为批处理文件中的条件中的等值线功能来计算并绘制相的调幅分解线。以下是计算Bcc相自旋线在批处理文件中的命令示例,图 3 所示Fe-Ni-Cr在700°C下的等温截面相图,红线为Bcc相的亚稳调幅分解线。
<condition>
<contour name="Spinodal" property="eVal(#1@Bcc)" start="0" stop="10" step="100" />
<equilibrium_type type="individual" />
<scanline_density value="1" />
<Hessian value="true" />
</condition>
[2021Mor] J.E. Morral, S. Chen, Stability of High Entropy Alloys to Spinodal Decomposition, J. Phase Equilib. Diffus., 42 (2021) 673–695
[2022Chen] S. Chen, R. Schmid-Fetzer, J.E. Morral, Calculation of Critical Points, J. Phase Equilib. Diffus., 43 (2022) 968-978.
[2022Kon] S.R. Koneru, K. Kadirvel, Y. Wang, High-Throughput Design of Multi-Principal Element Alloys with Spinodal Decomposition Assisted Microstructures, J. Phase Equilib. Diffus., 43 (2022) 753-763.