物理性质
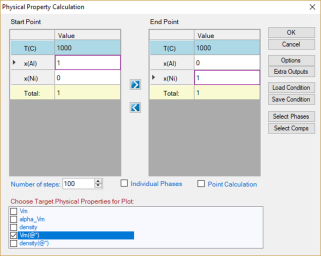
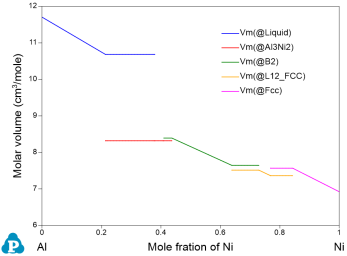
Pandat™软件中的物理性质计算功能可以计算摩尔质量、摩尔体积、密度、表面张力和粘度。其设置界面与热力学性质的计算相似,用户可以设置计算条件为线计算,并选择需要计算的性质,图 1所示为计算摩尔体积界面。默认图形即为所选择的物性性质,见图 2。如果选择多个性质,每个性质将被分别绘图。
各种性质的详细计算方法以及数据库的格式将在下面几节介绍。
例如,Al-Cu二元体系中的fcc相的组成为xAl = 0.9 和 xCu = 0.1,它的摩尔质量为:
|
|
(1) |
摩尔体积
如果在数据库文件中合理的定义了模型参数,Pandat™ 软件可以计算摩尔体积。纯组元的摩尔体积表达为温度和压力的函数,某相超额摩尔体积的表达形式与超额吉布斯自由类似。摩尔体积的单位是m3/mol-atoms。在(.TDB)数据库文件中,摩尔体积的格式为:
PARAMETER Vm(Fcc,Al;0) 298.15 +9.7743e-006
*exp(6.91213e-005*T+1.62267e-011*T**3+0.413484*T**(-1)); 3000 N !
PARAMETER Vm(Fcc,Fe;0) 298.15 +6.72092e-006*exp(6.97895e-005*T); 3000 N !
PARAMETER Vm(Fcc,Al,Fe:Va;0) 298.15 -3e-6; 3000 N !
某相摩尔体积的计算式为
|
|
(2) |
其中, 是用来计算该相的超额摩尔体积的参数。
体系中混合相的摩尔体积的计算式为
|
|
(3) |
其中 和
分别是
相的摩尔分数和摩尔体积。
注意,如果某相采用多点阵的化合物能量模型(CEF)来描述的,与吉布斯自由能类似,摩尔体积会被自动定义为T、P和位置数(y)的函数。这样就会引入多个端际相的摩尔体积,由此导致计算摩尔体积时不稳定。事实上,摩尔体积应该是摩尔分数(x)而非位置分数(y)的函数,因此,当采用CEF模型来描述某相时,建议单独定义该相的摩尔体积。该功能可由自定义摩尔体积性质来实现,请参见用户自定义性质。
以Al-Ni二元体系为例,键入“VARIABLE_X”来定义性质“Vm”:
Type_Definition v GES AMEND_PHASE_DESCRIPTION * VARIABLE_X Vm !
这意味着用如果一个相用了“v”这个由Type_Definetion定义的标识符,该相中Vm就以摩尔分数作为自变量。下例中定义了液相(Liquid) 和 L12_FCC 两个相的摩尔体积参数:
Phase Liquid %v 1 1 !
Parameter Vm(Liquid,Al;0) 298.15 +V_Al_Liquid; 3000 N !
Parameter Vm(Liquid,Ni;0) 298.15 +V_Ni_liquid; 3000 N !
Phase L12_FCC %v 2 0.75 0.25 !
Parameter Vm(L12_FCC,Al;0) 298.15 +0.935*V_Al_fcc; 3000 N !
Parameter Vm(L12_FCC,Ni;0) 298.15 +0.935*V_Ni_fcc; 3000 N !
在这种情况下,L12_FCC相的摩尔体积由下式计算:
|
|
(4) |
即使L12_FCC相用双亚点阵的CEF模型来描述,上式仍适用。详细信息请参见 用户自定义性质计算。
|
|
(5) |
体系中混合相的密度是由混合相的摩尔质量和摩尔体积计算得到的:
|
|
(6) |
粘度
Pandat™软件中具备计算液相粘度的功能。计算液相粘度的模型是Seetharaman和Du [1994See] 提出的半经验公式:
|
|
(7) |
其中
|
|
(8) |
其中V是溶体相的摩尔体积,h是Plank’s常数,N是Avogadro’s常数。ΔG*是活化吉布斯自由能,计算式如下:
|
|
(9) |
其中xi 和xj 分别是i和j组元摩尔分数, 是i组元的活化吉布斯自由能,
是混合吉布斯自由能。摩尔体积的计算已在上面章节中给出。纯组元的活化自由能在TDB数据库中给出,其格式为
Parameter ActivationEnergy(Liquid,Al;0) 298.15 15051+13.519*T; 2000 N !
表面张力
Pandat™软件另一个功能是计算液相的表面张力。液相表面张力的计算是利用Yeum等[1989Yeu]基于Butler模型[1932But]提出的半经验公式模型:
|
|
(10) |
其中si、a'i和ai 分别是组元i的表面张力、表面的活度和基体活度。Si为单层分子的表面积:
|
|
(11) |
其中b是几何因子,N是Avogadro’s常数,Vi是组元i的摩尔体积。此方法可以应用于计算多元合金的液相表面张力[1997Zha]。摩尔体积的计算与摩尔体积给出的相同。表面原子与内部原子的配位数之比b,由参数beta表示,其在TDB数据库的表示为:
Parameter Beta(Liquid,Al;0) 298.15 0.83; 2000 N !