析出相的长大
析出模块中内置了两种析出相的长大模型
(a) 简化的长大模型
在析出模块中,析出相颗粒的长大计算是基于扩散控制的假设,同时考虑了Gibbs-Thomson尺寸效应,采用了Morral和Purdy[1994Mor]提出的计算多元合金长大模型,在此基础上,进行修正以处理不同形态析出相的长大/溶解过程。弯曲界面,也就是球面或圆弧面的界面的移动速率,由下式给出
|
|
其中R是界面半径。R临界形核半径,和
分别是a (基体相)和 b(析出相)溶质浓度差的行向量和列向量,[M] 是基体的化学迁移矩阵。那么,方程 (1) 可进一步简化为
|
|
其中K是动力学参数, 是相变驱动力,定义为
,
是摩尔化学驱动力,
是由Gibbs-Thompson效应而引起的能量差。
(b) SFFK (Svoboda-Fischer-Fratzl-Kozeschnik) 模型
SFFK 模型 [2004Svo] 用一系列线性方程来描述体系中各析出相的半径和化学成分变化。体系由基体和析出相组成。析出相的成分由析出相的晶体结构和描述它的热力学模型决定,其表达式为,
|
|
其中参数aij 取0或1。
为了描述封闭体系在常温常压下的状态,选择状态参数qi。那么对于体系几何形貌和/或耦合过程,做以下几个假设,体系总的自由能G可由状态参数表达,总吉布斯自由能的损耗比率Q由 表示。在Q是比率
正定二次型的情况下,体系的演化是由总吉布斯自由能损耗Q的最大值给出的,Q是由
限制,以及其它一些与体系物理性质相关的限制条件。这种处理是基于Onsager 于1931年提出的热力学极值法则 [1931Ons1, 1931Ons2]。
令μ0i (i=1,...,n)是基体中组元i的化学势,μi (i=1,...,n) 是析出相中组元i的化学势。所有的化学势均表达为浓度Ci的函数。体系总的吉布斯自由能G表达为
|
|
其中 σ 是界面能,λ 是由析出相体积变化而引起的弹性能和塑性能的贡献。
体系的演化对应于总损耗比率Q的最大值,由 限制,其中,
|
|
此问题可表达为一系列的线性方程。通过解线性方程Ay=B,得到粒子长大速率和每一析出相浓度的改变速率。SFFK模型的详细介绍请参见[2004Svo]。
(c) 析出相形状演变
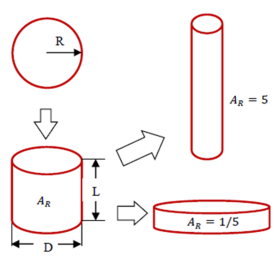
析出相长径比的演变驱动力源于析出相的各向异性错配应变和界面能的取向依赖性。在文献[2006Koz, 2008Svo]中,通过考虑形状因子及其在析出过程中的演变,对SFFK模型进行了修改。在该模型中,析出相形状由具有长度L和直径D的一族圆柱近似,如图 1所示。长径比AR(AR = L/D)用于描述析出相的形状。R是等效析出半径,其值为与圆柱形析出物具有相同体积的球形的半径。根据这个定义,AR值较小时代表盘形,而AR值大表示针形,如图 1所示。
在组织演化模块中,析出相在演化过程中的长径比AR 可视为常数或变量。在前一种情况下,基于AR 计算一组形状因子,生长模型也将做相应地调整[2006Koz]。形状因子S,圆柱形析出物的表面积与球形析出物的表面积之比,由下式给出:
|
|
析出相的界面迁移的形状因子K表达为 。析出相内部扩散的形状因子I为
。析出相外部扩散的形状因子O 由
给出。
对于后一种情况,对原始SFFK模型做了修正,并通过一组独立参数描述演化方程,包括有效半径(R),平均化学组成(Cki)和每个析出相的纵横比AR。这些参数的演化速率 ,
和
通过求解线性方程得到 [2008Svo]。在改进的SFFK中,形状演变由析出相的各向异性错配应变和界面能的取向依赖性决定。体系的总吉布斯自由能G的表达式如下,
|
|
第一项是基体相的吉布斯自由能的化学部分,第二项对应于储存的弹性能和析出相的吉布斯自由能的化学部分,第三项代表总析出相/基体界面能量。下标“0”表示与基体相关的量,例如,N0i 是基体中的组分i的摩尔数, μ0i是基体相的化学势。 λk(ARk)是由于析出相与基体之间的体积不匹配导致的弹性应变能的贡献,由方程 (6) 计算。μki是与cki 对应的析出相化学势。在本模型中,必须给出两个界面能量: (圆柱体的表面)和
(圆柱体底部和顶部)。形状因子
可通过计算与圆柱体具有相同体积的球体的等效半径
获得。
[1994Mor] J.E. Morral et al., “Particle coarsening in binary and multicomponent alloys”, Scr. Metall. Mater., 30 (1994): 905-908.
[2004Svo] J. Svoboda et al., “Modelling of kinetics in multi-component multi-phasesystems with spherical precipitatesI: Theory”, Mater. Sci. Eng. A, 385 (2004): 166–174.
[2006Koz] E. Kozeschnik et al., “Shape factors in modeling of precipitation”, Mater. Sci. Eng. A, 441 (2006): 68–72.
[2008Svo] J. Svoboda et al., “A model for evolution of shape changing precipitates in multicomponent systems”, Acta Mater., 56 (2008): 4896–4904.